Fizikalni modeli z Wolfram Language
Po dveh tednih je tu nov del gostujočih zapisov Allisona Taylorja iz Wolfram Research. Tokrat bo predstavil izgradnjo enostavnih fizikalnih modelov z uporabo Wolfram Lanugage. V kolikor niste seznanjeni s programi podjetja Wolfram na Raspberry Pi, si najprej oglejte prispevek o programu in namestitvi, nato pa lahko nadaljujete z branjem gostujočih zapisov.
Če ste se kdaj udeležili kakšnega tečaja fizike ali ste bili udeleženi v uri fizike, potem ste se najbrž učili o Newtonovi mehaniki. Ta vsebuje snov o ohranitvi energije in dinamike, harmoničnem gibanju in tako naprej. Če bi idealizirali se klasično gibanje lahko razčleni na dele enostavnih enačb, ki temeljijo na položaju, pospešku in hitrosti. Izpeljava teh enačb zahteva reševanje diferencialnih enačb – nekaj, kar Wolfram Language dela odlično s funkcijo NDSolve[].
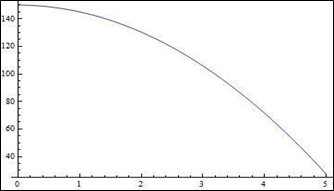
Na primer, za osnovni model padca potrebujemo zagotoviti prvotne pogoje – pospešek y je dan glede na gravitacijo, 9,81 m/s²; začetni položaj je 150 m; začetna hitrost y pa je 0. Iz teh pogojev je NDSolve[] zmožen izračunati hitrost za dano razdaljo.
|
1 2 3 |
freefall=NDSolve[{y''[t]==-9.81,y[0]==150,y'[0]==0},y[t],{t,0,5}]; Plot[y[t]/.%,{t,0,5}] |
ti dva ukaza nam prikažeta naslednje:
Torej, če sklepamo iz zgornjega primera in bi vrgli žogico iz višine 150 metrov, bi trajalo približno 5 sekund, da bi padla na tla. Enostavno! Zato lahko naredimo korak naprej s funkcijo WhenEvent[]. Če bi poskusili zmodelirati odbijanje žoge z roko, bi morali predelati enačbo gibanja vsakič, ko bi žoga dosegla nek “dogodek” ali spremenila pogoje v katerih deluje. Žogica leti iz zraka k tlom – vendar se ne moremo zanesti na enake vrednosti v primeru, da bi se žogica odbila od tal v zrak. Uporaba WhenEvent[] znotraj NDSolve[] vam omogoča, da navedete kaj se zgodi ob y[t] = 0, ali ko se žogica zadane ob tla. V tem primeru bi lahko rekli, da ko žogica zadane ob tla, in bo zamenjala smer potovanja, bo hkrati tudi spremenila hitrost na 95 %. Tako se bo vsakič, ko žogica zadane ob tla njena hitrost zmanjšala za 5 %. Vse to je mogoče narediti z NDSolve[], brez dodatnega dela za nas.
|
1 2 3 4 |
NDSolve[{y''[t]==-9.81,y[0]==5,y'[0]==0, WhenEvent[y[t]==0,y'[t]->-0.95 y'[t]]},y[t],{t,0,10}]; Plot[y[t]/.%,{t,0,10}] |
ta del kode izdela:
To, da smo te vrednosti pridobili samodejno izračunane pomeni, da lahko pravzaprav spremenimo tudi porabo energije po določenem času. Vzemimo izračunane vrednosti položaja in hitrosti ter jih vnesimo v osnovne enačbe za kinetično in potencialno energijo:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
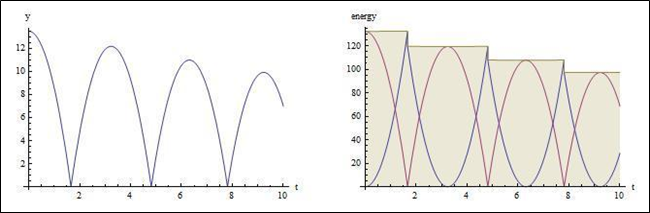
ball=NDSolve[{y''[t]==-9.81,y[0]==13.5,y'[0]==0, WhenEvent[y[t]==0,y'[t]->-0.95 y'[t]]},{y[t],y'[t]},{t,0,10}]; kin[v_]:=.5 v^2; pot[y_]:=9.8 y; energy[y_,v_]:=kin[v]+pot[y]; GraphicsGrid[{{Plot[y[t]/.ball,{t,0,10},AxesLabel->{"t","y"}], Plot[Evaluate[{kin[y'[t]],pot[y[t]],energy[y[t],y'[t]]}/.ball],{t,0,10}, Filling->{3->0},AxesLabel->{"t","energy"}]}}] |
te formule nam izdelajo spodnja grafa:
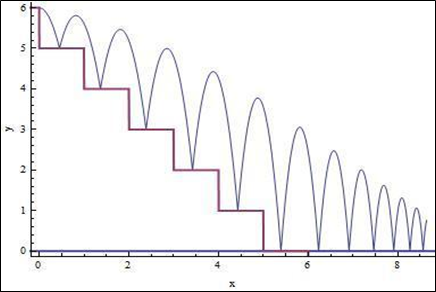
Graf na levi prikazuje položaj žogice, graf na desni pa potencialno energijo v rdeči barvi, kinetično energijo v modri barvi in skupno energijo v rjavi barvi. Naj omenim, da skupna energija po korakih pada, saj se energija z vsakim odbojem porablja. Gremo naprej! Kaj če se žogica sploh ni odbijala od tal? Kaj če bi namesto odbijanja na tla, žogica letela po stopnicah? V takšnih primerih se prav tako uporabijo enaki postopki s tem, da dodamo a[t] ter navedemo za koliko korakov v širini žogice se mora le-ta premakniti. Ko žogica doseže dno stopnic, uporabimo “RemoveEvent”, ki zaustavi nadaljnje izrisovanje stopnic na graf.
|
1 2 3 4 5 6 7 8 |
steps=NDSolve[{x''[t]==0,y''[t]==-9.8,y[0]==6,y'[0]==0,x[0]==0,x'[0]==1,a[0]==5, WhenEvent[Mod[x[t],1]==0,If[a[t]>0,a[t]->a[t]-1,"RemoveEvent"]], WhenEvent[y[t]==a[t],{{x'[t],y'[t]}->.9 {x'[t],-y'[t]}}]},{x[t],y[t],a[t]}, {t,0,15},DiscreteVariables->{a[t]}]; Show[ParametricPlot[Evaluate[{{x[t],y[t]},{x[t],a[t]}}/.steps],{t,0,15}, ImageSize->300],Plot[{0,Floor[6-x]},{x,-1,15},PlotStyle->Thick, Exclusions->None],Frame->{{True,False},{True,False}}, FrameLabel->{"x","y"}] |
ta koda naredi naslednje:
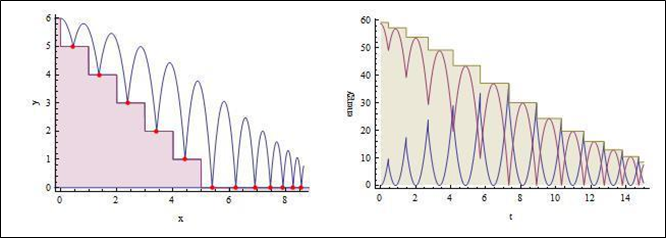
In ponovno bi lahko poleg prikazali porabo energije, Wolfram Language pa ima funkciji Reap[] in Sow[], ki nam pomagata pri določanju koordinat žogice ob vsakem odboju.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
{ballsteps,{points}}=NDSolve[{x''[t]==0,y''[t]==-9.8,y[0]==6,y'[0]==0, x[0]==0,x'[0]==1,a[0]==5,WhenEvent[Mod[x[t],1]==0,If[a[t]>0,a[t]->a[t]-1, "RemoveEvent"]],WhenEvent[y[t]==a[t],{{x'[t],y'[t]}->.9 {x'[t],-y'[t]}, Sow[{x[t],y[t]}]}]},{x[t],y[t],x'[t],y'[t],a[t]},{t,0,15}, DiscreteVariables->{a[t]}]//Reap; GraphicsGrid[{{Show[ParametricPlot[Evaluate[{{x[t],y[t]},{x[t],a[t]}}/.ballsteps], {t,0,15},ImageSize->300,Epilog->{Red,PointSize[Medium],Point[points]}], Plot[{0,Floor[6-x]},{x,-1,15},Filling->{2->0},Exclusions->None], Frame->{{True,False},{True,False}},FrameLabel->{"x","y"}], Plot[Evaluate[{kin[y'[t]],pot[y[t]],energy[y[t],Norm[{x'[t],y'[t]}]]}/.ballsteps], {t,0,15},Filling->{3->0},Frame->{{True,False},{True,False}}, FrameLabel->{"t","energy"},Ticks->None]}}] |
ti ukazi izdelajo sledeči graf:
Event[] znotraj NDSolve[] je lahko uporabljen za izris vseh vrst procesov – od tornih modelov za procesiranje signalov, celo do simulacije človeškega utripa srca. Omogoča vam vizualizacijo veliko zahtevnih okolij na enostaven, povezovalen način.