Najboljše enovrstične funkcije
Nov dan, nov del iz serije prispevkov, ki jih piše Allison Taylor iz Wolframa. Ti prispevki predstavljajo uvod v uporabo programa Mathematica, ki je za Raspberry Pi izšel poleg Wolfram Language in je privzeto nameščen na operacijskem sistemu Raspbian. Besedo prepuščamo Allisonu:
Na naših Wolfram Technology konferencah 2010 in 2011, so udeleženci pokazali svoje najboljše “enovrstičnice” – dele kode, ki so zapisani v manj kot eni vrsti in vsebujejo pod 140 znakov. Izhodni podatki so nato ocenjeni po njihovi kompleksnosti, uporabnosti in splošnem lepem izgledu. Predlogi so se izkazali kot precej različni, izzivajoči misli, predvsem pa so prikazali učinkovitost Wolfram Language. To tudi izgleda povsem primerno, saj majhni kosi močne kode ustrezajo majhni in močni napravi, mini računalniku Raspberry Pi. (Za zagon tega programa morate najprej s klikom na ikono Mathematica odpreti grafični vmesnik programa Mathematica na vašem Piju.)
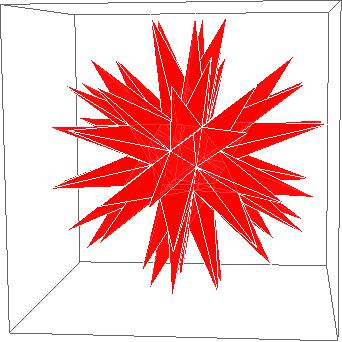
Echidnahedron (oziroma matematične konice), avtor Radko Kriz
Nismo si mogli pomagati, da vas nebi pričeli učiti nekaj zanimivega, kot je izdelava lepega in geometričnega logotipa, ki predstavlja Mathematico in Wolfram Research že več kot 25 let! Z nekaj matematičnega znanja in uporabe različnih geometrijskih teles je možno spisati funkcijo, ki celoto izriše kot razširjene konice.
|
1 |
Graphics3D[{Opacity[.8],Glow[RGBColor[1,0,0]],EdgeForm[White],Lighting -> None,PolyhedronData["Echidnahedron","Faces"]}] |
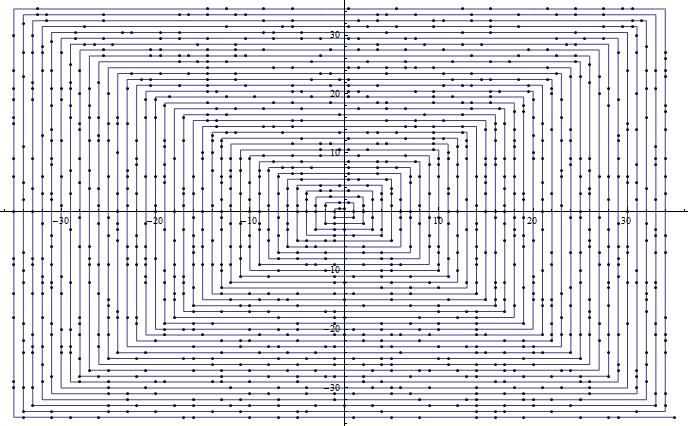
Ulam Spirala, avtor Dave Lawrence
Poleg podobne matematične teme je Ulam spirala odlična pot za prikaz praštevil. Spirala je prikazana na koordinatni ravnini celih števil, ki se začne v točki (0,0) in se nadaljuje z označevanjem vsake točke, kjer se nahaja praštevilo.
|
1 2 3 4 |
s = {Re@#, Im@#} & /@ Fold[Join[#1, Last@#1 + I^#2 Range@#2/2] &, {0}, Range@140]; ListPlot[s, Joined -> True, Epilog -> {Point /@ s[[Prime@Range@PrimePi@Length@s]]}] |
Sicer ne največja spirala, ki jo je doslej izdelal Stanislaw Ulam, vendar je vseeno lepa
Preizkus celega števila, če je praštevilo, avtor Sascha Kratky
Ko smo že ravno pri temi praštevil, je potrebno povedati, da obstaja veliko računalniških primerov, kjer tak del kode pride precej prav. Če poženete to funkcijo s katerokoli številko, vam bo vrnila rezultat tipa bool – True ali False.
|
1 2 3 |
RegExPrimeQ[n_Integer] := ! StringMatchQ[StringJoin[Table["1", {Abs[n]}]], RegularExpression["^1?$|^(11+?)\\1+$"]] RegExPrimeQ[17] |
Izdelajte svojo Borg kocko, avtor Alex Hirsbrunner
Zagotovo ste si vedno želeli izdelati svojo kocko. S povezovanjem nekaj naključno ustvarjenih kock različnih velikosti in barv, ta koda ustvari prav vašo različico Borg kocke, ki vaše prijatelje še bolj navduši.
|
1 2 3 4 5 6 7 8 |
p := Random[]; r = RotateLeft; Graphics3D[ Table[{RGBColor[.2, p, .2], Cuboid[l = r[{z, p, p}, a], l + r[p/ 8 {Sign[z - .5], p, p}, a]]}, \ {z, {0, 1}}, {a, 0, 2}, {6!}]] |
Fraktali, avtor Stephan Leibbrandt
Z nekaj vrsticami kode lahko izdelate šklatlo v obliki srca, ki ima žice in vzmeti.
|
1 2 3 4 5 |
Image@Compile[{}, Block[{i, x, p}, Table[i = 0; x = 0. I; p = r + I c; While[Abs@x Tanh[Power[i/9^3, (7)^-1]], {c, -1, 1, .01}, {r, -2, 1,.01}]]][] |
Gumijasta raca, avtor Paul Abbott
S to kreacijo pa bomo tudi končali članek. Narejena je iz vrste sferičnih funkcij in je zares ljubka, kajne?
|
1 2 3 4 |
SphericalPlot3D[ Log[\[Theta]] + Sin[\[CurlyPhi]], {\[Theta], 0, 2 \[Pi]}, {\[CurlyPhi], 0, 2 \[Pi]}, Boxed -> False, Axes -> False, PlotStyle -> Yellow, Mesh -> None, PlotPoints -> 30] |
Ste dobili inspiracijo? Pokažite nam tudi kakšno vašo “enovrstičnico”, ki se sklada z Raspberry Pijem.